The Most Important Algorithms - An Overview
Once I too, was a beginner in coding. But things changes with time.
Here I'm guiding all beginners by providing these 'must have' algorithms.
Here I'm guiding all beginners by providing these 'must have' algorithms.
1. Searching
Searching is most basic algorithm that we learn even from our junior level. Our main aim in this algorithm is search a particular element in a given data structure.
Types Of Searching :
Search starts at the first element in the list and continues until either the item is found in the list or entire list is searched.
A binary search is a dichotomic divide and conquer search algorithm.Every iteration eliminates half of the remaining possibilities. This makes binary searches very efficient - even for large collections. Our implementation relies on recursion, though it is equally as common to see an iterative approach.
2.Sorting
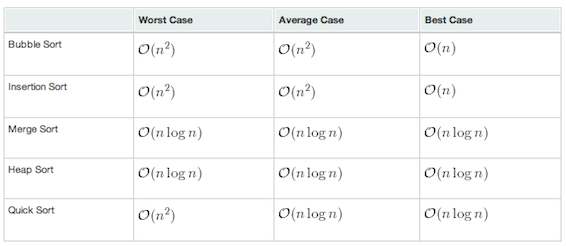
Sorting is technique of arranging data in a particular fashion for e.g. ascending ,descending, logical order.Sorting by insertion is the simplest method, and doesn’t require any additional storage. Shell sort is a simple modification that improves performance significantly. Probably the most efficient and popular method is quicksort, and is the method of choice for large arrays.Other Sorting techniques are - bubble, merge ,shell sort.
Fig : Comparison of different sorting algorithms.3. Tower of Hanoi
You can say , tower of hanoi is a mathematical puzzle but ,obviously, can also be solved by algorithm. Problem consists of 3 disc holders(rod) and n discs of different sizes.
 |
| Tower Of Hanoi- initial situation |
Now, the objective of the puzzle is to move the entire stack to another disc holder (rod) , but following these 'small' conditions:
i) At a time or for one move ,only one disc must be moved.
ii)We can't place any larger disc on top of smaller disc.
i) At a time or for one move ,only one disc must be moved.
ii)We can't place any larger disc on top of smaller disc.
4. Buchberger's algorithm
It was invented by Austrian mathematician Bruno Buchberger. This problem is as follows:
Input: A finite setB of polynomials.
Input: A finite set
Output: A finite Gröbner basis G such that the linear combinations of elements of B are precisely the same as the linear combinations of elements of G . We call such a G equivalent to B.
Buchberger's algorithm provides a means to transform an arbitrary set of polynomials into an equivalent Gröbner basis. Therefore, questions about some set of polynomials arising in an application can be answered by first using Buchberger's algorithm to compute an equivalent Gröbner basis and then answering the question for the Gröbner basis.
5. Newton's Method
Also named as Newton–Raphson method- formulated by Isaac Newton and Joseph Raphson
Efficient algorithm for finding approximations to the zeros (or roots) of a real-valued function. Newton's method is also a well-known algorithm for finding roots of equations in one or more dimensions. It can also be used to find local maxima and local minima of functions.
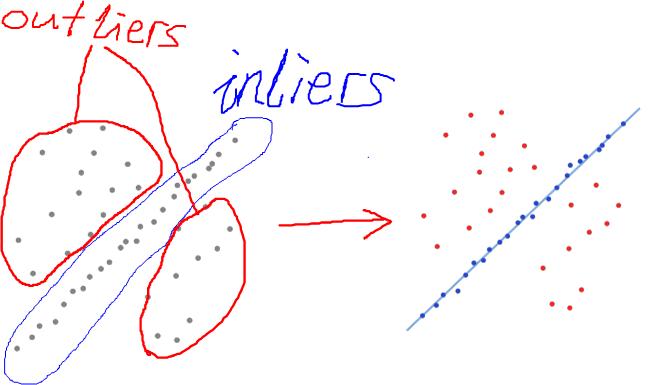
6. RANSAC
RANSAC is an abbreviation for "RANdom SAmple Consensus". It is an algorithm to estimate parameters of a mathematical model from a set of observed data which contains "outliers" i.e. the data which do not fit the model. A basic assumption is that the data consists of "inliers", i. e., data points which can be explained by some set of model parameters, and "outliers" which are data points that do not fit the model.
7.Schönhage-Strassen algorithm
(developed by Arnold Schönhage and Volker Strassen in 1971)
In mathematics, the Schönhage-Strassen algorithm is an asymptotically fast method for multiplication of large integer numbers.Its complexity in Big O notation, O(N log N log log N) compared to pen-paper multiplication of O(n^2). The algorithm uses recursive Fast Fourier transforms in rings with 22n + 1 elements, a specific type of number theoretic transform.
8.Solving a system of linear equations
Systems of linear equations belong to the oldest problems in mathematics and they have many applications, such as in digital signal processing, estimation, forecasting and generally in linear programming and in the approximation of non-linear problems in numerical analysis. An efficient way to solve systems of linear equations is given by the Gauss-Jordan elimination or by the Cholesky decomposition.
9. Simplex algorithm
The journal Computing in Science and Engineering listed it as one of the top 10 algorithms of the twentieth century.The Simplex Method is "a systematic procedure for generating and testing candidate vertex solutions to a linear program." (Gill, Murray, and Wright, p. 337) .The simplex method is an iterative procedure, solving a system of linear equations in each of its steps, and stopping when either the optimum is reached, or the solution proves infeasible.